Integral Berechnen Ohne Ein Integral Zu Lösen

Einführung

Das Berechnen von Integralen ist ein zentrales Thema in der Mathematik, insbesondere in der Analysis. Doch nicht immer ist es notwendig, ein Integral direkt zu lösen, um seinen Wert zu bestimmen. Es gibt verschiedene Methoden und Tricks, mit denen man das Ergebnis eines Integrals bestimmen kann, ohne die klassische Integration durchzuführen. Diese Anleitung zeigt dir Schritt für Schritt, wie du mit mathematischen Überlegungen, Symmetrien, bekannten Flächeninhalten und cleveren Umformungen Integrale berechnen kannst, ohne sie explizit zu lösen.

Integral Berechnen Ohne Ein Integral Zu Lösen

Zeitabschätzung

• Für das Verständnis und die Anwendung der Methoden: ca. 30–60 Minuten
• Für das Üben an eigenen Beispielen: ca. 1–2 Stunden

Materialliste

• Papier und Stift (optional: kariertes Papier für Skizzen)
• Taschenrechner (optional, für numerische Überprüfungen)
• Formelsammlung oder Mathematikbuch (optional)

Gesamtkosten: 0–10 €

Schritt-für-Schritt-Anleitung

1. Das Integral und die Aufgabenstellung genau analysieren

• Lies die Aufgabenstellung sorgfältig und notiere das gegebene Integral.
• Überprüfe, ob das Integral bestimmte Eigenschaften aufweist (z.B. bestimmte Grenzen, spezielle Funktionen).
• Notiere dir, ob es sich um ein bestimmtes oder unbestimmtes Integral handelt.

Das Integral und die Aufgabenstellung genau analysieren

2. Symmetrien und Eigenschaften der Funktion erkennen

• Prüfe, ob die Funktion gerade, ungerade oder periodisch ist.
• Überlege, ob das Integral über einem symmetrischen Intervall (z.B. von -a bis a) verläuft.
• Nutze bekannte Eigenschaften: Das Integral einer ungeraden Funktion über einem symmetrischen Intervall ist immer 0.

Symmetrien und Eigenschaften der Funktion erkennen

3. Flächeninhalte geometrisch interpretieren

• Überlege, ob die Funktion einen bekannten Flächeninhalt beschreibt (z.B. Dreieck, Rechteck, Kreis).
• Zeichne eine Skizze der Funktion und des Integrationsbereichs.
• Berechne den Flächeninhalt mit geometrischen Formeln statt mit Integration.

Flächeninhalte geometrisch interpretieren

4. Bekannte Integrale und Standardwerte nutzen

• Prüfe, ob das Integral einem bekannten Standardintegral entspricht (z.B. ∫₀^π sin(x) dx = 2).
• Vergleiche die Funktion mit einer Liste von Standardintegralen aus der Formelsammlung.
• Setze den bekannten Wert direkt ein, ohne das Integral zu berechnen.

Bekannte Integrale und Standardwerte nutzen

5. Substitutionen und Variablentransformationen erkennen

• Überlege, ob durch eine geschickte Substitution das Integral vereinfacht werden kann.
• Prüfe, ob sich das Integral durch eine Variablentransformation auf ein bekanntes Integral zurückführen lässt.
• Notiere die Substitution und überprüfe, ob das neue Integral leichter zu bewerten ist.

Substitutionen und Variablentransformationen erkennen

6. Numerische Abschätzung oder Grenzwerte verwenden

• Falls das Integral nicht exakt berechenbar ist, schätze den Wert mit einer numerischen Methode (z.B. Trapezregel).
• Überlege, ob der Grenzwert des Integrals für bestimmte Parameter einfach zu bestimmen ist.
• Vergleiche das Integral mit einer bekannten Funktion, um eine Abschätzung zu erhalten.

Numerische Abschätzung oder Grenzwerte verwenden

7. Integral mit Hilfe von Symmetrieeigenschaften sofort bestimmen (Beispiel)

• Beispiel: ∫₋₁¹ x³ dx
• Erkenne, dass x³ eine ungerade Funktion ist und das Intervall symmetrisch um 0 liegt.
• Schließe daraus, dass das Integral 0 ist, ohne zu rechnen.

syms x
int(x^3, x, -1, 1)
% Ergebnis: 0

Integral mit Hilfe von Symmetrieeigenschaften sofort bestimmen

8. Integral als Flächeninhalt eines Kreises bestimmen (Beispiel)

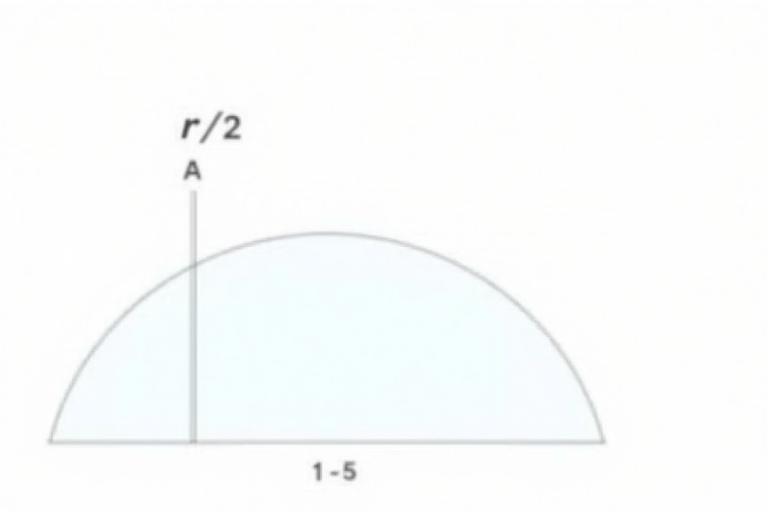
• Beispiel: ∫₋₁¹ sqrt(1 - x²) dx
• Erkenne, dass sqrt(1 - x²) die obere Halbkreishälfte mit Radius 1 beschreibt.
• Berechne den Flächeninhalt der Halbkreisscheibe: (π·1²)/2 = π/2.

A = pi/2

Integral als Flächeninhalt eines Kreises bestimmen

9. Integral mit bekannter Stammfunktion und Grenzen (Beispiel)

• Beispiel: ∫₀^π sin(x) dx
• Die Stammfunktion von sin(x) ist -cos(x).
• Setze die Grenzen ein: -cos(π) + cos(0) = -(-1) + 1 = 2.

syms x
int(sin(x), x, 0, pi)
% Ergebnis: 2

Integral mit bekannter Stammfunktion und Grenzen

10. Integral durch Vergleich oder Abschätzung bestimmen

• Vergleiche das Integral mit einem ähnlichen, bekannten Integral.
• Nutze Abschätzungen, um den Wert des Integrals einzugrenzen.
• Überprüfe, ob das Integral zwischen zwei bekannten Werten liegt.

Integral durch Vergleich oder Abschätzung bestimmen

Tipps

• Überprüfe immer, ob die Funktion spezielle Eigenschaften wie Symmetrie oder Periodizität besitzt, bevor du mit aufwendigen Rechnungen beginnst.
• Zeichne dir eine Skizze der Funktion und des Integrationsbereichs – oft wird dadurch die Lösung offensichtlich.
• Nutze Formelsammlungen und Tabellen mit Standardintegralen, um Zeit zu sparen und Fehler zu vermeiden.